MBR challenge

In this challenge, we are presented with a 512 KB file. Given that it’s a reverse engineering challenge, my initial step was to determine the file type.

ms02@ms02:/home/ms02/Downloads$ file OS.bin
OS.bin: DOS/MBR boot sector

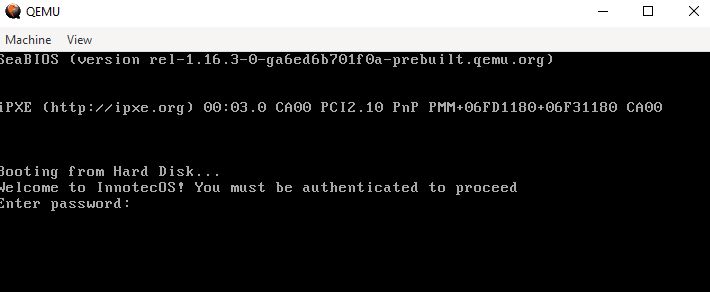
Upon inspecting the file, it was identified as an MBR (Master Boot Record) bootloader. To proceed, I decided to emulate the file using QEMU and verify if it could be executed.

.\qemu-system-i386.exe -drive format=raw,file=C:\Users\Adrian\Downloads\OS.bin

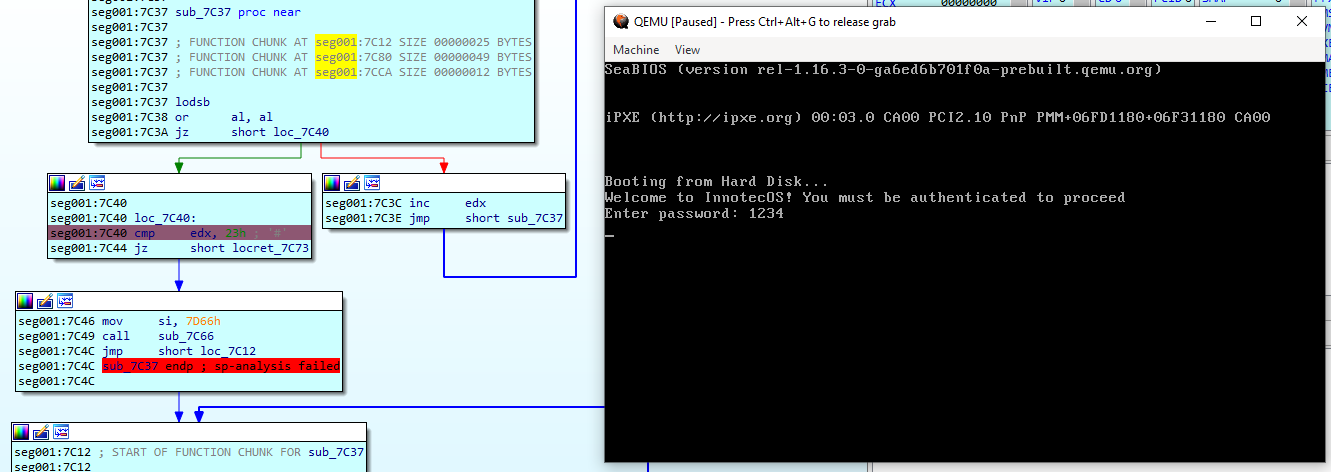
After setting up the emulation environment, I ran the bootloader, which prompted for a password. When any password was input, an error message was displayed.

QEMU on first execution

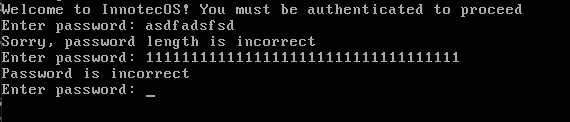
Typing some random password, this message is shown:

Incorrect length

The error message suggested there was a password length check before the final verification. To find the required password length, I experimented with different lengths. Eventually, a different message appeared when a 35-character password was entered. Thus, the password length was determined to be 35 characters.

Correct length

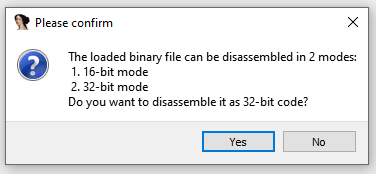
With this knowledge, I began analyzing the binary using IDA. Check that the loading offset must be 0x7C00 as MBR starts on that address:

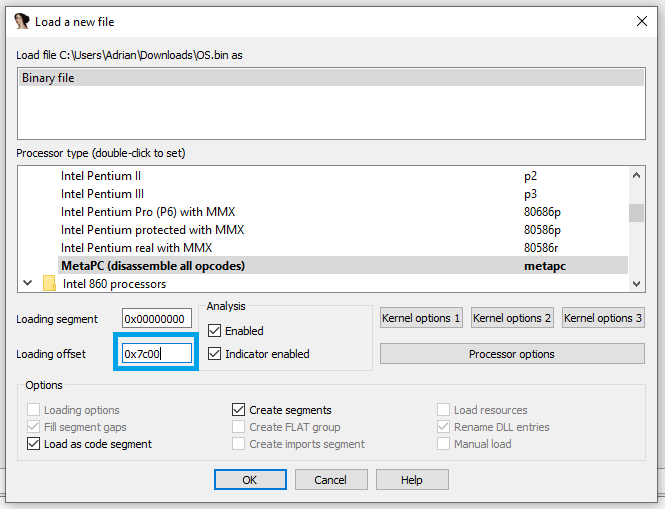Loading binary with correct offset

In order to remain compatible, all x86 BIOS architecture systems start with the microprocessor in an operating mode referred to as real mode. This mode works in 16-bit for compatibility, so let’s load it as 16-bit.

The next step was to connect QEMU with the IDA debugger. By enabling debugging mode in QEMU with the -s flag, a remote GDB server starts on port 1234 by default. The -S option freezes the CPU on startup.

.\qemu-system-i386.exe -s -S -drive format=raw,file=C:\Users\Adrian\Downloads\InnotecOS.bin

QEMU paused on startup

I attached the debugger to the process using localhost and connected to port 1234.

Remote debug on IDA config

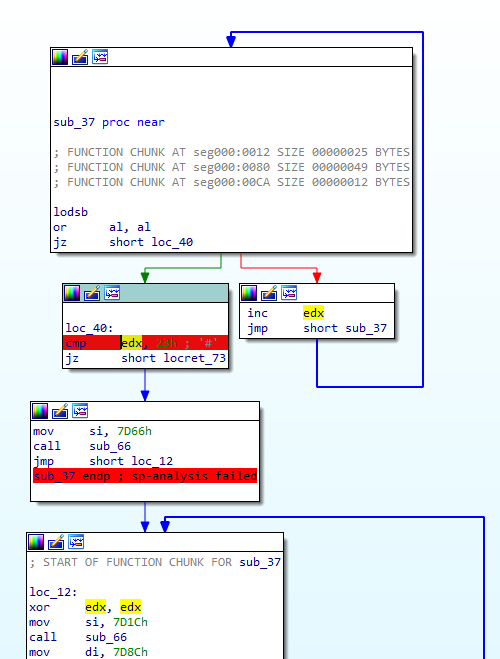
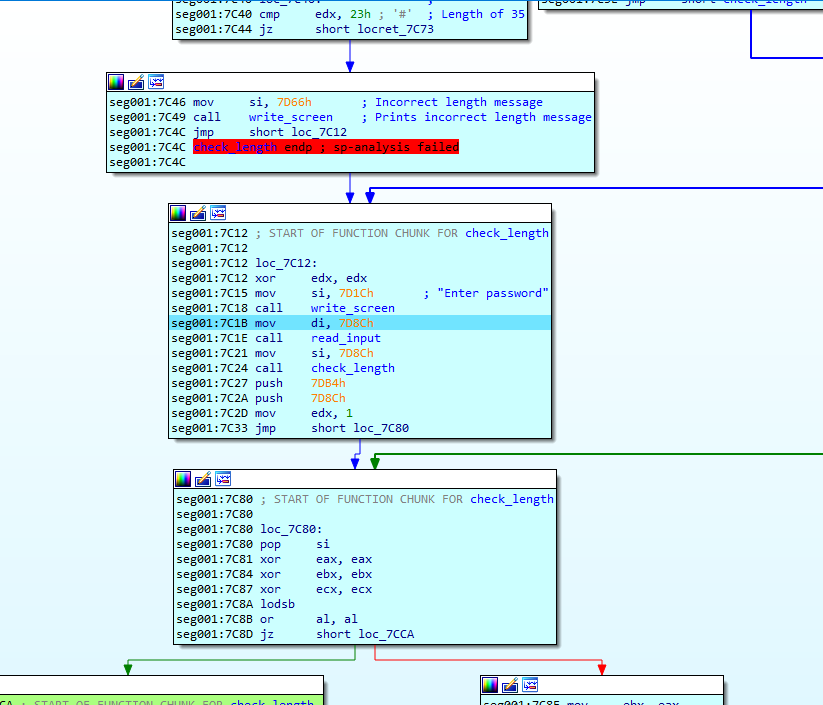
As identified earlier, the password should be 35 bytes long. As we can see below, the lodsb instruction loads the next character of the input password and increments the counter (EDX) until it encounters a null byte. The length is checked with a CMP operation between the EAX register and 0x23 (35 in decimal). I set a breakpoint at this address to begin tracing the code.

Password length check

Stopped on breakpoint

Looking forward, IDA helped identify two functions for printing on the screen and reading input (the password). Renaming these functions provided clarity.

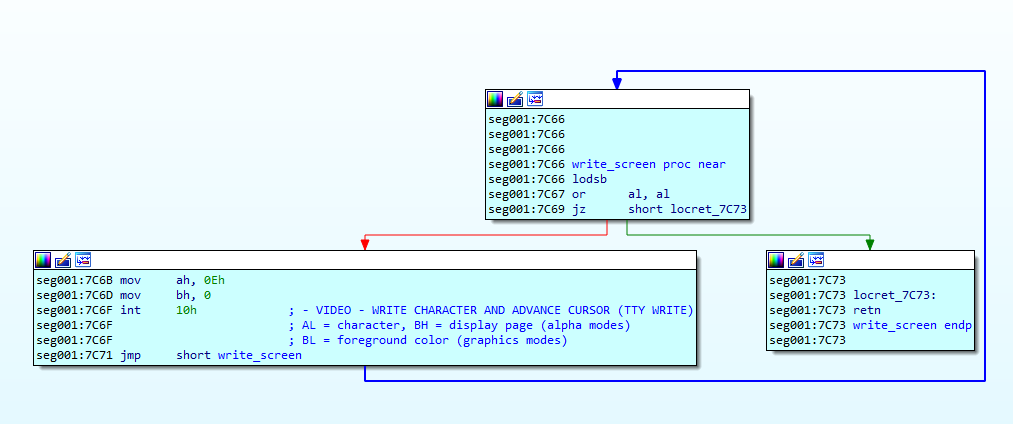Function to print on screen 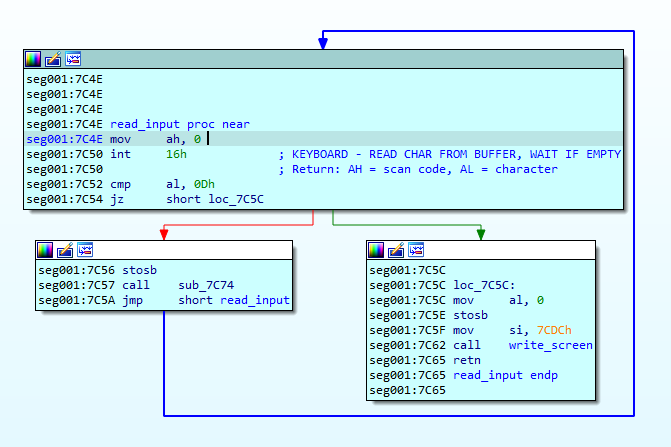Function to get chars

We can also identify the blocks where the correct and incorrect password messages are displayed:

• Green indicates the correct password block.
• Red indicates the incorrect password block.

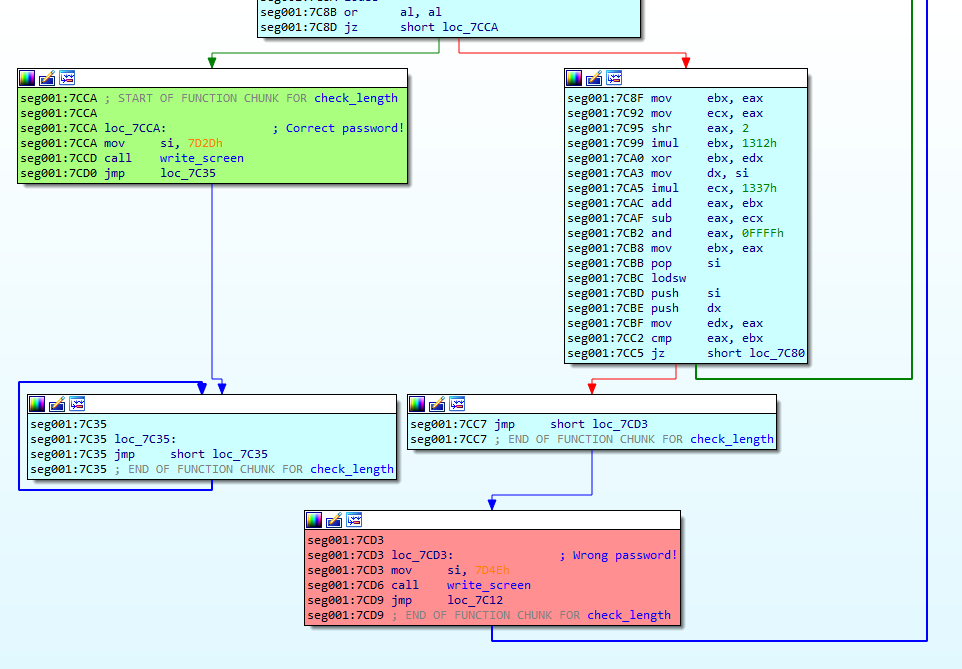
The main part is as follows: it prints the message “Enter password:” and waits for the input at 0x7C1E. Then, it checks the length of the input string at 0x7C24.

Main part

At this stage, we know the program requests a password, checks its length, and if it’s not 35 bytes, displays “Wrong length password.” If the password is 35 characters long, it checks each character.

Password checking algorithm

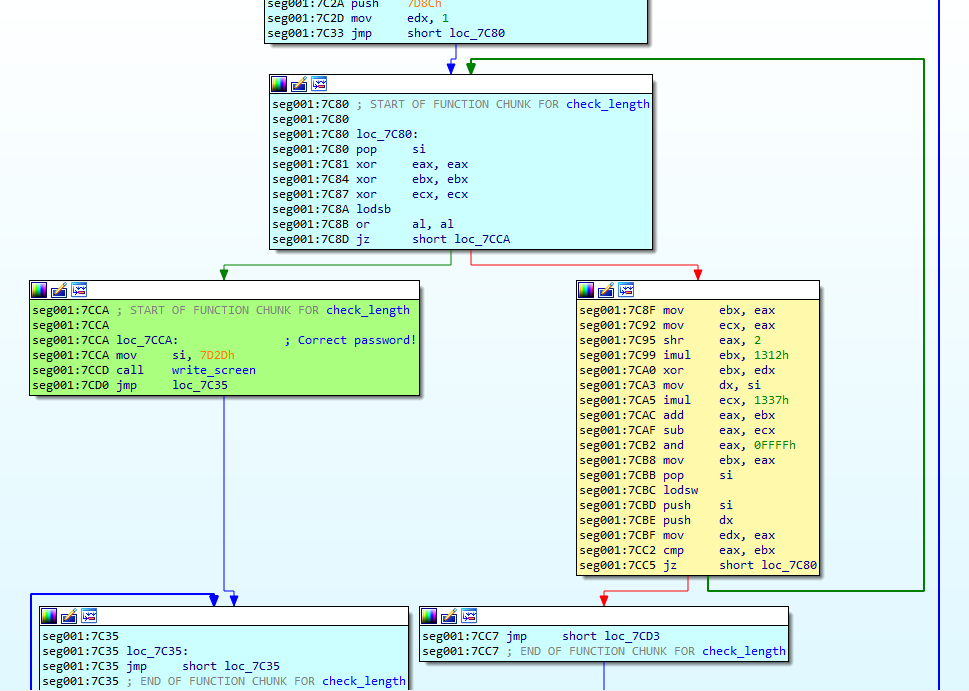
The algorithm for password verification is found here. It’s a loop that checks each character of the password. If the CMP at 0x7CC2 fails, the loop exits, displaying an incorrect password message. If the character is correct, it moves to the next one until it reaches the null byte. Upon successful verification, the correct password message is shown.

Let’s dive into the algorithm step by step. First it loads the first input character of the password into EAX register on 0x7C8A. It checks if its a null byte (the end of string) at 0x7C8B. If it’s not, it performs some operations. On 0x7CBC, it loads the content of the memory address pointed by ESI into EAX. This is the value that will be compared with the input character after some operations.

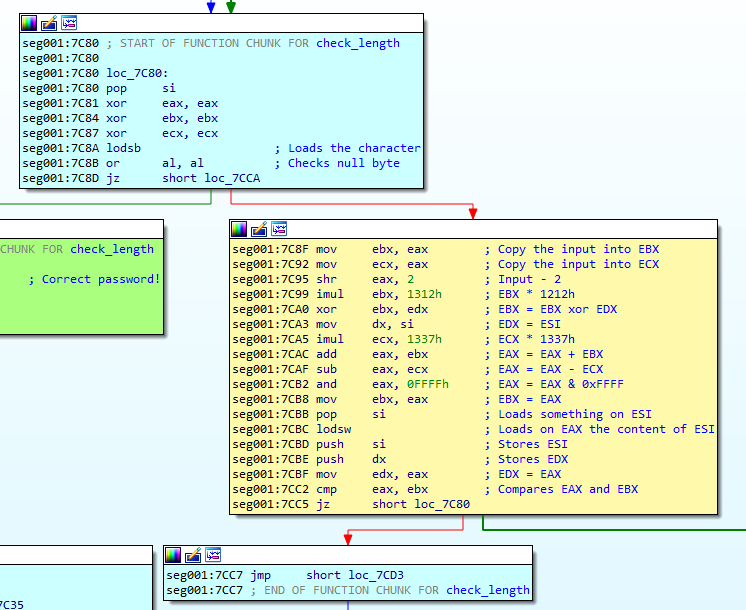Commented password checking algorithm

I tried to write a function to solve this, or at least, simplify it. First of all was to write a pseudocode or python code:

EAX = 'X' # Input password character
EDX = '' # Something unknown
ESI = '' # Memory address of the input

# Loads ESI from the stack

EBX = EAX # Copy the value of EAX
ECX = EAX # Copy the value of EAX

EAX = EAX >> 2 # Bitshifting EAX

EBX = EBX * 4882 # Multiplying EBX with 4882 (decmal)

EBX = EBX ^ EDX # XOR EBX with EDX. EDX unknown.

EDX = ESI # Copy ESI on EDX

ECX = ECX * 4919 # Multiply ECX * 4919 (decimal)

EAX = EAX + EBX

EAX = EAX - ECX

EAX = EAX & 0xFFFF # Clean upper 16 bits of EAX

EBX = EAX # Copy EAX to EBX

# Load into ESI top of stack.

# Load the content of the memory address pointed by ESI

# Stores the ESI on stack.

# Stores the EDX on stack.

EDX = EAX

if (EAX == EBX):
    print("ok")

I tryed to simplify it with something more descriptive:

original_input_char = 'X' # Input password
EDX = '' # Unkown
input_memory_pointer = '' # Memory address of the input (ESI)

# Loads ESI from the stack

temporal_storage = original_input_char # (EBX)
temporal_storage_extra = original_input_char # (ECX)


input_char = original_input_char >> 2 # Bit shifting

temporal_storage = temporal_storage * 4882
temporal_storage = temporal_storage ^ EDX # Unknown value yet

EDX = input_memory_pointer

temporal_storage_extra = original_input_char * 4919 # Operate temporal_storage

input_char = input_char + temoral_storage

input_char = input_char - temporal_storage_extra

input_char = input_char & 0xFFFF

temporal_storage = input_char

# Load into ESI from the stack.

input_char = [input_memory_pointer]

# Stores the ESI on stack.

# Stores the EDX on stack.

EDX = input_char

if (input_char  == temporal_storage):
  print("Ok")

Substituting the elements and trying to simplify even more, we could obtain the following equation:

(original_input_char >> 2) + ((original_input_char * 4882) ^ EDX) - (original_input_char * 4919) & 0xFFFF = memory_value

Here we have a simplified ecuation or algorithm that it’s applied. There are two values which i’m not sure yet what they are. This values are the EDX register and the memory_value. Let’s debug the code to understand this two operands.

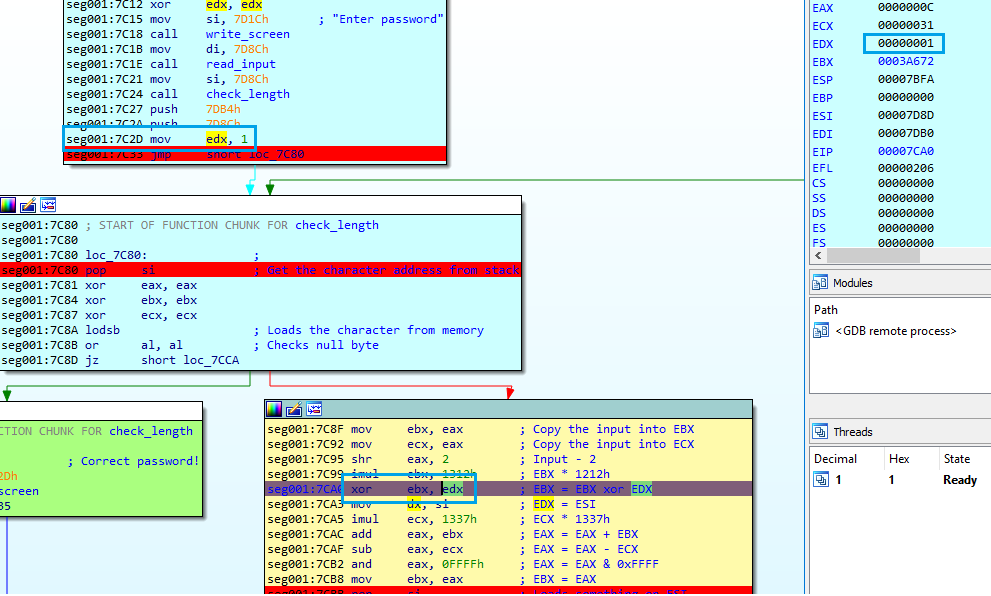
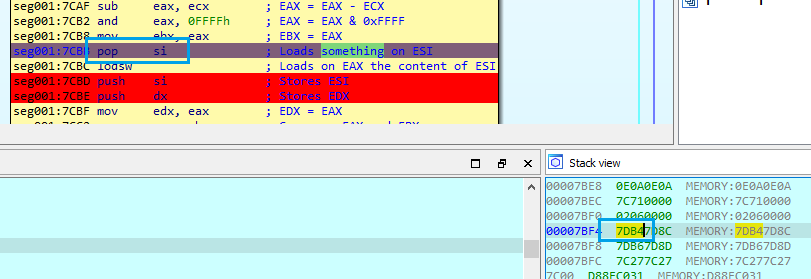
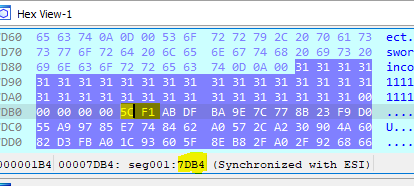
On first iteration, EDX is 1. The memory pointer (ESI) is loaded from stack. The first value is 0x7DB4 (because it’s SI register).

With the next instruction, it will load the content of the address 0x7DB4 into EAX:

Memory values EAX register

This is the value that will be compared with the operated input_char:

(original_input_char >> 2) + ((original_input_char * 4882) ^ 1) - (original_input_char * 4919) & 0xFFFF = 0xF15C

So now we have the complete operation for the first character. Lets keep trying to understand how it works. On next character, it will be:

EDX = 0xF15C

Memory address: 0x7DB8 with the value 0xDFAB.

The ecuation will be:

(original_input_char >> 2) + ((original_input_char * 4882) ^ 0xF15C) - (original_input_char * 4919) & 0xFFFF = 0xDFAB

That means that, on every iteration, the algorithm gets the input char to run the calcs. EDX value for the first iteration is 1, and on the next iterations it’s the previous value of EAX, that is, the previous retrived from memory, the right side of the equaton.

This values will be from the address 0x7DB4 to the address 0x7DF9 (69 bytes + null byte) as we are comparing 2 bytes on the right side of the equation.

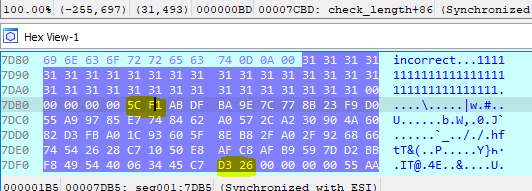Values to be compared with input password

Due to some of the operations such as xor, bitwise, etc., it is not possible to easily solve the equation to obtain the value of original_input_char. What occurred to me was to bruteforce since there are not a big amount of characters to test (255*35).

I wrote this code for solve it:

# Data from memory
results = [0xf15c, 0xDFAB, 0x9EBA, 0x777C, 0x238b, 0xd0f9, 0xa955, 0x8597, 0x74e7, 0x6284, 0x57a0, 0xa22c, 0x9030, 0x604A, 0xd382, 0xa0fb, 0x931c, 0x5f60, 0xb88e, 0xa02f, 0x922f, 0x6668, 0x5474, 0x2826, 0x10C7, 0xE850, 0xC8AF, 0xb9af, 0x7D59, 0xBBD2, 0x49f8, 0x4054, 0x3406, 0xc745, 0x26d3]

def bruteforce(result, edx):
    for val in range(32, 126): # Printable chars
        computed_value = ((val >> 2) + ((val * 0x1312) ^ edx) - (val * 0x1337)) & 0xFFFF
        if computed_value == result:
            return chr(val)
    return None

def main():
    counter = 0
    for result in results:
        if counter >= 1:
            edx = results[counter-1]
        else:
            edx = 1
        found_char = bruteforce(result, edx)
        counter+=1
        print(found_char, end='')

if __name__ == "__main__":
    main()

Running it, here is the flag:

flag{W0w_y0U_mUsT_b3_4_R34l_H4x0R!}